Метрики и несбалансированные выборки¶

04.04.2017¶

Мельник Богдан¶

Метрики и задачи связаны¶

Регрессия
Классификация
Временные ряды
Ранжирование

Метрики регрессии¶

Mean squared error¶

$$MSE = \frac{1}{l} \sum_{i = 1}^{l}{(a(x_i) - y_i)^2}$$

Во многих библиотеках для регрессии является метрикой по умолчанию
Иногда используется $RMSE = \sqrt{MSE}$ для получения ошибки такой же размерности, что и у таргета
Штрафует большие ошибки сильней, чем маленькие

Mean absolute error¶

$$MAE = \frac{1}{l} \sum_{i = 1}^{l}{\left| a(x_i) - y_i \right|}$$

Иногда используется вместо $MSE$ из-за большей устойчивости к выбросам
Интуитивно понятна

Сравнение MSE и MAE¶

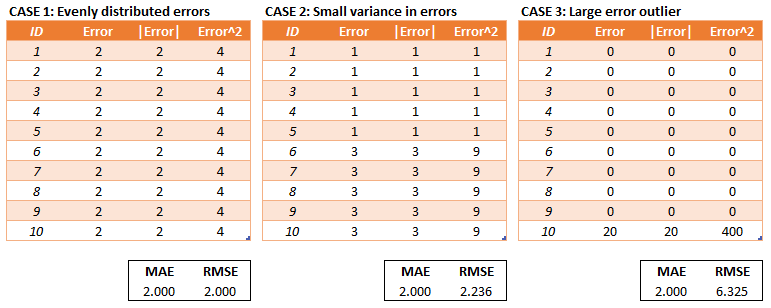
Недостатки MSE и MAE¶

MSE и MAE позволяет сравнивать качество моделей между собой
Даёт плохое представление о том насколько хорошо решена задача
Решение с $MSE = 10$ может быть плохим, если $y \in (0, \dots, 10)$, или хорошим, если $y \in (1000, \dots, 10000)$

Коэффициент детерминации¶

$$R^2 = 1 - \frac{\sum_{i = 1}^{l}{(a(x_i) - y_i)^2}}{\sum_{i = 1}^{l}{(\bar{y} - y_i)^2}}$$

Позволяет получить нормированную оценку качества
Измеряет долю дисперсии, объясненную моделью, и имеет значение от $0$ до $1$
Если значение близко к $1$ — модель полностью объясняет дисперсию $y$
Если значение близко к $0$ — модель сопоставима по качеству со средним предсказанием

Метрики классификации¶

Матрица ошибок¶

	y = 1	y = 0
a(x) = 1	True Positive (TP)	False Positive (FP)
a(x) = 0	False Negative (FN)	True Negative (TN)

Используется для вывода многих метрик для задач классификации

Accuracy¶

$$acuraccy = \frac{1}{l} \sum_{i = 1}^{l}{[a(x_i) = y_i]} \\ acuraccy = \frac{TP + TN}{TP + FN + FP + TN}$$

Доля правильных ответов классификатора
Самый простой способ оценить качество классификации
Вычисляется по умолчанию при использовании cross_val_score в задачах классификации
Плохо работает, если классы несбалансированы

In [20]:

print(accuracy_score(y_balanced, np.zeros_like(y_balanced)))
print(accuracy_score(y_unbalanced, np.zeros_like(y_unbalanced)))

0.480499719708
0.974691358025

Точность и полнота¶

$$precision = \frac{TP}{TP + FP} \\ recall = \frac{TP}{TP + FN}$$

Точность показывает какая доля объектов, выделенная классификатором как положительная, действительно является положительной
Полнота показывает какая доля положительных объектов была выделена классификатором как положительная
Если $a(x) = [p(x) > t]$, то обычно при увеличении $t$ точность будет расти, а полнота падать

In [225]:

precision, recall, thresholds = precision_recall_curve(y_balanced, y_hat)
thresholds = [0] + thresholds.tolist()
plot(thresholds, precision, label='precision');
plot(thresholds, recall, label='recall');
legend(); xlabel('Threshold'); ylabel('Precision or recall');
title('Precision and recall for balanced dataset');

F-score¶

$$F = \frac{2 * precision * recall}{precision + recall}$$

Способ объеденить точность и полноту в одной метрике
Принимает значения от $0$ до $1$
Точность, полнота и F-score подходят для оценки качества на несбалансированных выборках
Необходимо выбирать порог $t$ в случае вещественного ответа $p(x)$

In [224]:

thresholds = np.linspace(0, 1, 100)
scores = [f1_score(y_balanced, (y_hat > t).astype(np.int)) for t in thresholds]
plot(thresholds, scores, label='F-score');
scatter(thresholds[np.argmax(scores)], np.max(scores), label='Maximum');
legend(); xlabel('Threshold'); ylabel('F-score');
title('F-score for balanced dataset');

ROC AUC¶

Способ оценки качества классификации без необходимости подбора порога

In [63]:

roc_auc_score(y_balanced, y_hat)

Out[63]:

0.70524418709213299

ROC AUC¶

Использует только порядок ответов, соответственно любое монотонное преобразование не меняет значение метрики

In [64]:

print(roc_auc_score(y_balanced, y_hat))
print(roc_auc_score(y_balanced, 100 * y_hat + 5))
print(roc_auc_score(y_balanced, y_hat ** 2))

0.705244187092
0.705244187092
0.705244187092

ROC AUC¶

Для модели возвращающей случайную вероятность $AUC = 0.5$

In [228]:

hist([roc_auc_score(y_balanced, np.random.random(size=y_balanced.shape[0])) for i in range(1000)], bins=25);
xlabel('AUC');
title('Distribution of AUC for random classifier');

ROC AUC¶

Имеет несколько интерпретаций
- Площадь под кривой изображающую зависимость $TPR = \frac{TP}{TP+FN}$ от $FPR = \frac{FP}{FP+TN}$
- Вероятность $p(x_1) < p(x_2)$ для двух случайных объектов, у которых $y_1 = 0$ и $y_2 = 1$
- Зависит от доли дефектных пар

In [227]:

fpr, tpr, _ = roc_curve(y_balanced, y_hat)
plot(fpr, tpr, lw=2);
plot([0, 1], [0, 1], linestyle='--');
xlim([0.0, 1.0]); ylim([0.0, 1.05]);
xlabel('False Positive Rate'); ylabel('True Positive Rate');
title('ROC for balanced dataset');

ROC AUC¶

Также как и $accuracy$ неинформативен в случае несбалансированных выборок, но при этом лучше ведёт себя, если передать в качестве ответов метки доминирующего класса

In [95]:

print(np.mean(cross_val_score(LogisticRegression(), x_unbalanced, y_unbalanced, cv=StratifiedKFold(10))))
print(roc_auc_score(y_unbalanced, np.zeros_like(y_unbalanced)))

0.9771648334
0.5

Logloss¶

$$logloss = \sum_{i = 1}^{l}{y_i * \log( p(x_i) ) + (1 - y_i) * log(1 - p(x_i))}$$

Логарифм вероятности получить исходный вектор ответов
В отличие от ROC AUC важны значения, а не порядок

Logloss¶

Одно близкое к нулю значение под логарифмом может сильно испортить всю метрику

In [113]:

log_loss(y_balanced, y_hat, eps=0)

Out[113]:

0.62378626588930719

In [114]:

y_hat[0] = 1 - y_balanced[0]
log_loss(y_balanced, y_hat, eps=0)

Out[114]:

inf

Больше метрик¶

Существует огромное количество других метрик
Зачастую специфичны для определённого типа задач
Описание некоторых других метрик на Kaggle

Работа с несбалансированными выборками¶

Можно считать, что выборка несбалансирована, когда размеры классов отличаются более, чем в 10 раз
Больший класс называют доминирующим, меньший класс называется минорным
Зачастую можно повысить качество с помощью
- Корректировки весов объектов
- Исскуственной модификации датасета

In [116]:

np.mean(y_unbalanced)

Out[116]:

0.025308641975308643

Оценка качества при несбалансированных выборках¶

Accuracy и AUC дают близкие к $1$ значения, которые слабо меняются при изменении модели
F-score гораздо более чувствительна к изменениям модели

In [120]:

print(np.mean(cross_val_score(LogisticRegression(), x_unbalanced, y_unbalanced, cv=cv, scoring='accuracy')))
print(np.mean(cross_val_score(LogisticRegression(), x_unbalanced, y_unbalanced, cv=cv, scoring='roc_auc')))

0.981562067774
0.993632917551

In [121]:

np.mean(cross_val_score(LogisticRegression(), x_unbalanced, y_unbalanced, cv=cv, scoring='f1'))

Out[121]:

0.63985523564465452

Подбор порога без изменений в обучении¶

Подберём порог для F-score
Лучший $F = 0.676510$ при $\alpha = 0.356783$

In [145]:

plot(alphas, scores, label='F-score');
scatter(0.5, get_score(0.5, y_unbalanced, y_hat), label='0.5');
scatter(alphas[np.argmax(scores)], np.max(scores), label='optimal');
xlabel('alpha'); ylabel('F-score'); legend();

Корректировка весов¶

Большинство моделей в scikit-learn имеют параметр class_weight
Можно передавать словарь {label: вес} или "balanced"
По умолчанию каждый объект имеет вес $1$

In [151]:

clf = LogisticRegression(class_weight='balanced')
y_hat = cross_val_predict(clf, x_unbalanced, y_unbalanced, cv=cv, method='predict_proba')[:, 1]

Подбор порога с class_weight¶

Подберём порог для F-score
Лучший $F = 0.717647$ при $\alpha = 0.954773$

In [155]:

plot(alphas, scores, label='F-score');
scatter(0.5, get_score(0.5, y_unbalanced, y_hat), label='0.5');
scatter(alphas[np.argmax(scores)], np.max(scores), label='optimal');
xlabel('alpha'); ylabel('F-score'); legend();

Модификация датасета¶

Искуственное изменение пропорции меток в датасете
- Undersampling — уменьшение размера доминирующего класса
- Oversampling — увеличение размера минорного класса
Для работы с несбалансированными выборками существует удобная библиотека imbalanced-learn
Предоставляет большой выбор методов undersampling'a и oversampling'a
Имеет API, позволяющее встраиваться в cross_val_predict и cross_val_score

Undersampling¶

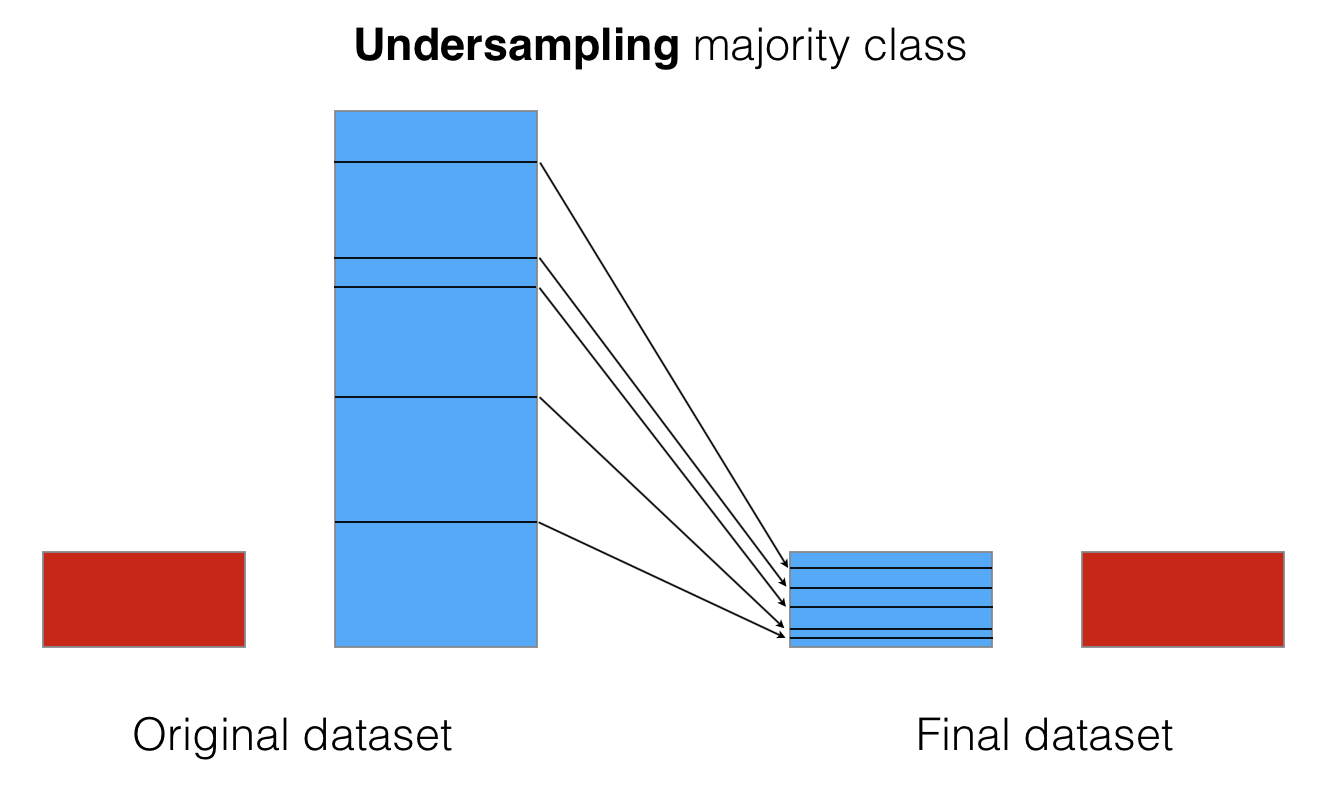
Уменьшение размера доминирующего класса undersampling

Undersampling¶

Случайное выбрасывание объектов imblearn.under_sampling.RandomUnderSampler
Замена доминирующих объектов на их кластера с помощью KMeans imblearn.under_sampling.ClusterCentroids
Много других способов с их описаниями

Oversampling¶

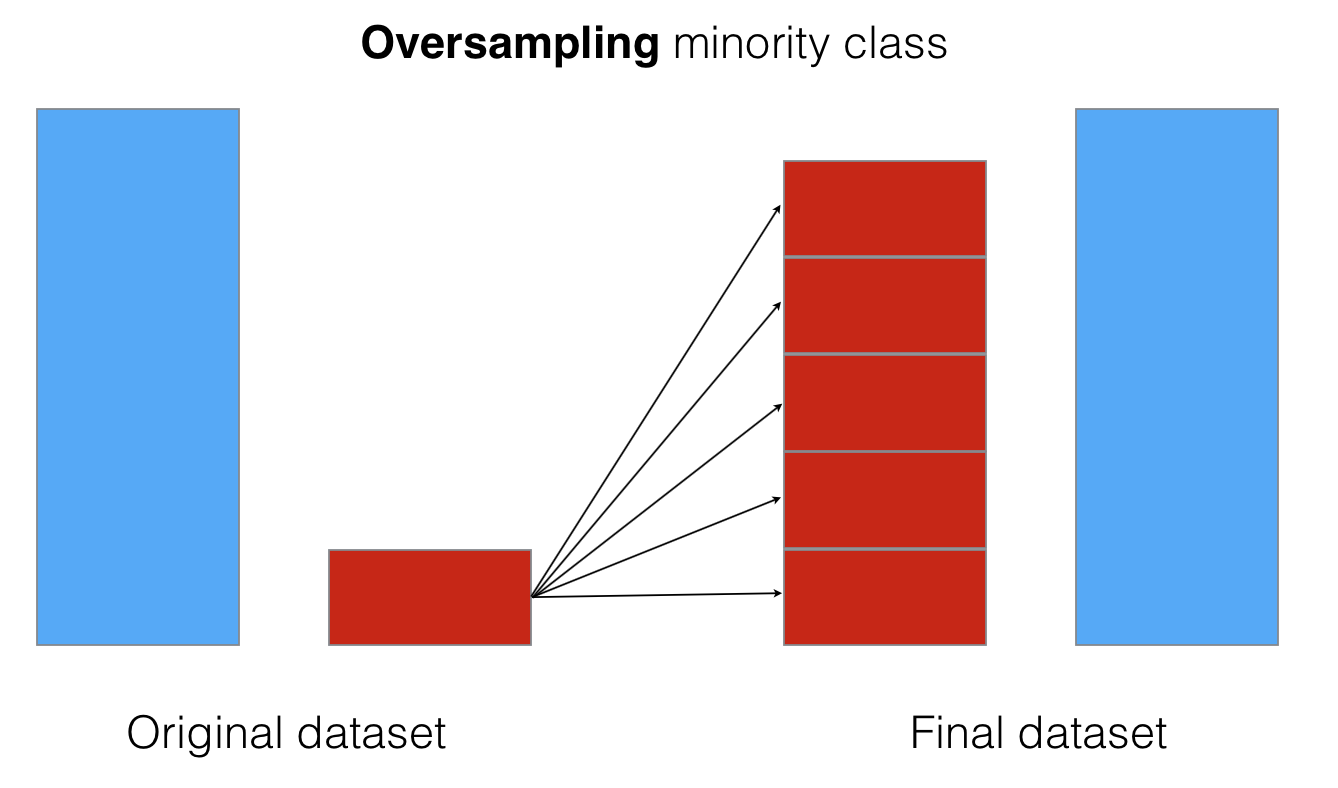
Увеличение размера минорного класса oversampling

Oversampling¶

Случайное повторение объектов из минорного класса imblearn.over_sampling.RandomOverSampler
Генерация новых объектов с помощью линейной комбинации существующих imblearn.under_sampling.SMOTE
Много других способов с их описаниями

Пример работы с imblearn¶

In [217]:

clf = pipeline.make_pipeline(over_sampling.SMOTE(), LogisticRegression())
y_hat = cross_val_predict(clf, x_unbalanced, y_unbalanced, cv=cv, method='predict_proba')[:, 1]

Выбор порога для SMOTE¶

Лучший $F = 0.691068$ при $\alpha = 0.452261$

In [220]:

plot(alphas, scores, label='F-score');
scatter(0.5, get_score(0.5, y_unbalanced, y_hat), label='0.5');
scatter(alphas[np.argmax(scores)], np.max(scores), label='optimal');
xlabel('alpha'); ylabel('F-score'); legend();